技術コラム

　第１回　ウォ-ムの効率 【ウォーム歯車の効率を求める式】
昔から、平歯車やハスバ歯車とウォ－ム歯車の効率を比較した言い方に、 「平歯車やハスバ歯車は、コロガリだから効率が良く、ウォ－ム歯車は、滑り接触だから効率が悪い」と言われています。 これは少し言い方が間違っていると思います。特に滑り接触だから効率が悪いという言い方はどうかと考えます。あえて言うなら、 「滑りの悪いウォ－ム歯車は効率が悪い」と言うべきでしょう。何故なら滑りの良いウォ-ムは経験上非常に効率が良いからであります。

では滑りの良し悪しとは何を意味するのか?。右の欄は、ウォ－ム歯車の効率の計算式です。この計算式をみると効率は摩擦角に支配 されていることが分かります。摩擦角はさらに摩擦係数に支配されていますので、摩擦係数が小さければ滑りがよく効率が良いといえます。 ・・ということで「滑りの良いウォ－ム歯車は効率が良い」と言う事になります。		 η=tanγ／tan（γ+ρ）
η：効率　γ：ウォ－ムの進み角　ρ：摩擦角
ここで、
ρ=tan-1（μ）
μ：摩擦係数
上の式で摩擦係数μを限りなく小さくすれば、効率ηは限りなく１００％に近づきます。
※ウォームとウォームホイールの歯面をつるつるにすることです。
第2回　セルフロックの常識 セルフロックが効く状態とは
セルフロックという言葉は、ウォ－ム減速機以外あまり使われない言葉で、この意味するところ（定義とでも言うか）は、
「機械的又は電気的なブレ－キ機構がない状態において，出力側（この場合ウォ－ムホィ－ルの側）から入力軸（ウォ-ム軸） を回転することができない状態にある」ことを言う。

で、ウォ－ム減速機の全てがセルフロックできる訳ではない。一部の仕様を 満足したものだけがセルフロックすることができる。そのまえに何でセルフロックが必要かというと、定義のところでブレ－キ機構 を減速機の使用環境の中で使うことができない場合や、吊物いわゆるウインチなどで降下の時の加速制限効果などや止めた状態を ブレ－キ無しで保持したい・・・など色々ある。
　ところで、ウォ－ムのセルフロックとは結構いい加減？・・確実なセルフロックはないと言われる。 その理由は、第一回で記載したウォ－ムの効率の式にある。
 出力軸（ウォームホィール）からウォームを回す時の伝達効率を計算する次式に、
η=tan（γ-ρ）／tanγ　において
γ≦ρ　の場合、
効率ηは０か負になるためウォ－ムホィ－ルからウォ－ムを回転することができない。
これがセルフロックの理論である。
で、なんで確実でないかというとこの式の中に摩擦が関与するからである。
実際にセルフロック仕様で設計したものをある程度の範囲で製作することはできるが、 ウオ－ムは使用しているうちになじんで摩擦係数が変化したり、あるいは回転速度によって噛み合い歯面の滑り速度が変化すると 摩擦係数も変化する。・・ということでなかなか確実なセルフロックというのはありえない。が他の減速機にないウォ－ム減速機の 最大の特徴でもある。

以上　次回に続く

第三回　セルフロックの境界

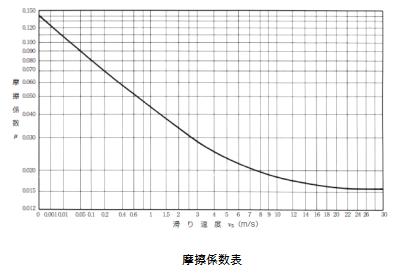
セルフロックの効く境界はどこにあるのか考えてみる、又確実に効くところがあるのか。前回記載したように、 理論的にセルフロックするのは、γ≦ρ　の場合である。ウォ－ムの進み角γより摩擦角ρが大きくなったときである。 で摩擦角は、

　　　ρ=tan-1（μ）

で求められる。μは摩擦係数である。動的（ウォ－ムが動いているとき）には 特定しにくいが、静止しているときにはＢＳ規格、経験値などから一定の条件の下に求めることができる。 （摩擦係数表は下段右枠内参照。）
ＢＳ規格（イギリス）では、μ=0.135

をとる。
ただし、ウォ－ムは肌焼入れ後研削したもので、ウォ－ムホィ－ルは りん青銅という組み合わせの時である。この値を前出の式に代入すると、
　　　ρ=tan-1(0.135)=7.688゜
これより小さい進み角のウォ－ムを設計すればセルフロックは効くことになる。
 ただし、ウォ－ムを使っていると歯面のなじみが進み摩擦係数がこれより小さくなる。 このためにメ－カ－によってセルフロックの設計仕様が異なる。例えば、なじみを考慮してμ=0.1で設計すると、

　　　ρ=tan-1（0.1）=5.710゜

になる。

摩擦係数を知ることができれば境界を計算できると考える、 摩擦係数は効率測定して前出の式から逆算することができる。 ただし、どのように設計しても不確定な要素を含んでいるのでメ-カ-から保障されるものではない。 一般的にセルフロックの効果のある減速比は1/40、1/50､1/60であるが、効率の良いウォ－ムでは、1/50,1/60ぐらいになる。 最近では舞台装置、ホ－ムエレベ－タなど吊物関係では、あまりセルフロックの効果を期待されない。
それよりもむしろ効率を要求される、特に起動効率・・・・。 　
ウォ－ムの特色を生かした設計がされないのは少しさびしい気がするがこれも時代の流れか、残るはカム、インデックスの駆動源 としてのみか・・・

次回は、ウォ－ムの起動効率

第四回　動かない減速機

舞台装置の吊物用に設計した減速機が動かないという。見に行って調べてみても問題はなかった。設計内容を聞いてみるとどうもインバ－タの容量不足である事がわかった。どういう計算をしていたのか見せてもらうと、必要動力を計算するときに減速機のランニング効率を用いていたことが判った。平歯車やハスバ歯車では、ランニング効率と起動効率の差はそれほど大きくないが、ウォ－ム減速機の場合は、ランニング効率に対して起動効率は半分ぐらいになる。このためにインバ－タなど起動トルクが小さい動力源を使用する場合、ランニング効率で計算すると動かないことになる。 要するに、効率が半分になるから起動トルクが倍以上かあるいは容量の大きいの動力源を用いる必要があった。 ちなみにウォ－ム減速機の起動効率の計算は、

η=tanγ／tan(γ+ρ)　の式において、摩擦角を

ρ=tan-1(0.135)=7.688゜

にとって計算すればよい。これは回転数(滑り速度)="０"のときの摩擦係数0.135の値を とって計算している。		 静的効率ともいうが、起動効率とほとんどイコ－ルである。
さて原因は判ったがその対策は大変であった。インバ－タの方は変更できないから ウォ－ムで何とかしてくれということになった。
当時高性能歯形のウォ－ムを開発していたので、まずその歯車諸元で再設計した。 それに加えウォ－ムに鏡面加工を施し、さらに歯当りを最初から６０％以上出すために新品のホブを二日間研ぎ続けた。
その結果、 ウォ－ム減速機は動き始めた。

次回は、”最強の歯形”

第五回　最強の歯形－その１

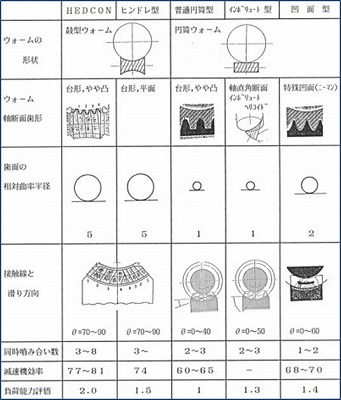
歯形の話の前にウォ－ム歯車の形態の分類と性能について考えてみる。 ウォ－ム歯車は、大きく分けると円筒形と鼓形に分けることができるがさらに詳細に分けると下図のようになる。ウォ－ムの形状が 円筒か鼓形かで円筒ウォ-ム、鼓形ウォ-ムと呼んでいるのが慣例である。
　一般的に、円筒ウォ-ムより鼓形ウォ-ムの方が性能がはるかに高いと言うのが常識である。しかし、同じ鼓形と呼ぶ図２と図４では 性能が大きく違うことをご存知だろうか。また、図１の円筒ウォ－ムより図４の鼓形ウォ-ムの性能が一部の能力を除いては同等以下 であることを知る人は少ない。
　今回は、それぞれのウォ-ムの特徴と性能の比較についてお話しする。ただし、図３はほとんど使用例がないので省略する。

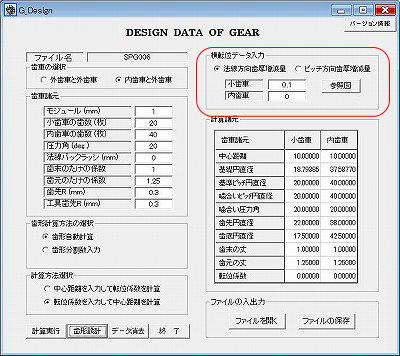
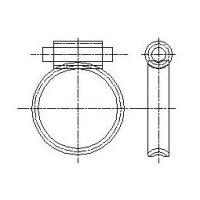
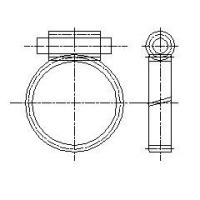
図１　円筒ウォ-ムと鼓形ホィ－ル 図２　鼓形ウォ-ムと鼓形ホィ-ル 図３　円筒ウォ-ムと円筒ホィ－ル 図４　鼓形ウォ-ムと円筒ホィ－ル

図１の円筒ウォ-ムと図２のの鼓形ウォ－ムについて比較して見ると、鼓形は 噛み合い率及び歯面の相対曲率半径が大きいので伝達トルクが一般的な円筒ウォ-ムの２倍から４倍程度ある。又、同時接触線が滑り 方向に対して立っているので歯面の潤滑性がよく効率が良いとされている。理論的にはそうであるが、円筒ウォ-ムを鏡面加工した ものと比べるとほとんど差は無い。
　また、起動効率においては円筒ウォ-ムの方が効率が良い。鼓形のウイ－クポイントである。理由は単純で、ウォ-ム軸の径が端部で 大きくなるため進み角γが小さくなりその結果摩擦係数が同じであれば効率が低くなる、このために起動するためのモ-タが大きくなり コスト高となる。　次に、図４の鼓形ウォ－ムの特徴であるが、このウォ-ムは図１の円筒ウォ-ムを丁度ひっくり返したものであることが図からわかる。 円筒ウォ－ムを円筒ホィ－ルとし、鼓形ホィ-ルを鼓形ウォ-ムに置き換えたものである。なぜこのような形にしているのかは、製作性 の問題とだけしておく。
　このウォ-ムは噛み合い率は多いが、歯当り面積が極端に小さく接触圧が大きくなるので伝達能力は、円筒ウォ-ムに比べて同等か あるいは低い。特に高速回転ではよくない。起動効率も悪いがランニング効率も低い。ただし、低速回転やセルフロックを要求される 用途には向いている。又、噛み合い率が高いので静的な強度が円筒ウォ-ムに比べて優れている。
　以上に述べたように、全ての面で鼓形ウォ-ムが優れているわけではない。鼓形の性能を出すには、鼓形ウォ-ムと同形のボブを製作 して創成歯切りを行う必要がある。(舞ツ－ルなどで歯切りされた鼓形ホィ－ルでは歯当りが小さく能力が低い）そして、この工具の 製作が困難であるのと同時に工具寿命が短いため非常にコストが高くなる。このような難しいウォ－ムよりも製作性の良い円筒ウォ-ム の能力を上げることを考えれば良いのではないか。

次回は、"最強の歯形－その２"

第六回　最強の歯形－その２

円筒ウォ－ムの歯形としては、５種類ほどある。その中で現在実際に使われているのは、ＪＩＳ３形（台形）、ＪＩＳ４形 （インボリュ－トヘリコイド）、ニ－マン歯形（凹形）である。性能比較では、
　　　　　　　　　　　　　　　　３形＜４形＜ニ－マン歯形
とされているが、３形と４形はさほど差が無く、材料・潤滑油などで逆転する場合もある。ニ－マン歯形は、凹形のウォ－ムの歯形と 凸形のホィ－ルの歯形が噛み合うため、面圧応力が小さくなり伝達トルクを大きくできる。３形、４形に比べ１．５から２倍近く伝達 トルクを高くとることができる。また潤滑性も良好なため効率も良いとされている。ただ、大きくプラス転位（１モジュ－ル）されて いるため噛み合い率が前者のウォ－ムよりも小さくなる欠点がある。現在のところ円筒ウォ－ムの中では、最強の歯形である。しかし、 製作性の問題から価格が高く（鼓形より少し安い）、高級品であまり一般的には使われていない。最近では、ウォ－ムホィ－ルの材料に 耐摩耗材料を使用したり、ＰＡＧ系の高性能合成潤滑油を使用することで３形歯形ウォ－ムでも従来の１．５倍の伝達トルクを実現でき るようになっているのでそれほど差がなくなってきた。ただ、ニ－マン歯形のウォ－ムもこの材料と潤滑油を使用すればその差は縮まら ない。
　　Ｗ／Ｎ歯車という歯車がある。Ｗ／Ｎというのはウイルドハ－バとノビコフという人の名前である。いづれの人も円弧歯形の歯車を 提案したり、開発実用化した。この歯形は、ヘリカルギヤなどに使われている。歯形の歯末が凸、歯元が凹の円弧歯形である。当然負荷 能力は高くなる。このような歯形をウォ－ムに適用した場合どうなるのか・・・・・。当然ニ－マン歯形のように負荷能力は高くなる。 また、ニ－マンのように転位しなければ噛合い率が大きくなるためニ－マンより高い能力が期待できる。問題は、製作性とコストである。

第七回　最強の歯形－その3

　右図は、サイクロイド曲線を基準ピッチラインにおいて結合して作成したウォ－ムの基準ラック歯形である。この歯形を工具歯形として ホィ－ルを創成すると凹と凸の噛合いになり非常に大きなトルクを伝達できる。しかしながらラックの基準ピッチ点で圧力角が０になる ためウォ－ムホィ－ルを創成すると歯形干渉が起こり出口側の歯先部が創成されない。この歯形干渉への対策として、サイクロイドの 回転が２０゜のところで上下の歯形を結合することでこの問題を解決することができた。
実際に、下記の諸元で試作した。
心　　　 間：　１００ｍｍ
モジュ－ル：　５.４、４.１
減　速　比：　１／１０、１／４０
負荷テスト
入力回転数：　１８００ｒｐｍ
出力トルク：　９７～１２０ｋｇｆ・ｍ
効率
起動効率　　　　：１／１０で７２％　，１／４０で４５％
ランニング効率 ：１／１０で９４％　，１／４０で８７％
無負荷騒音 ：４０～５０ｄｂ
一般的に高性能と言われるウォ－ムに比べても非常に性能が高いという結果であった。 出力トルクでは、同サイズの鼓形ウォ－ムとほぼ同等である、効率では上回っている。
 問題は、製作性であるが、ウォ－ムを研削するＮＣのネジ研削盤と同歯形を持つ ホブ以外は台形歯形のウォ－ムを製作するのとそれほど違いは無い。最近では、ウォ－ムのネジ研削盤はほとんどＮＣ化されているので、 歯形の専用ソフトを導入すれば製作するのは困難ではない。歯筋クラウニングも台形歯形と同じ方法を適用できる。台形歯形の製作性と 鼓形に勝るとも劣らない性能を持つ歯形、これこそ最強の歯形であると考える。

第八回　汎用ウォームの歯形の問題

　一般的に使われているウォームの歯形はⅢ形歯形がほとんどであるが、ではこのウォームと噛み合うウォームホィールの歯形は Ⅲ形歯形であろうか？
ウォームホィールの歯形は、ホブの歯形によって決まるのでほとんどの場合、圧力角２０゜のラック歯形であることからⅠ形歯形になる。 ウォームはⅢ形でホィールはⅠ形のかみ合わせとなる。Ⅲ形歯形のウォームは、下図のように円錐形状のカッター又は砥石で仕上げられる為、 歯先や歯元で砥石の加工干渉により直線歯形とはならない。
１条ウォームでは、その影響はほとんどない。２０゜のラック歯形である。２条ウォームでは、モジュールや進み角、砥石径にもよるが 0.03～0.05mm程度の干渉で歯が丸くなるが、この量が歯形修正となりちょうど都合がよい。問題は、３条以上のウォームである。進み角が 18゜以上になるとモジュールや砥石径にもよるが干渉量が一桁アップする。この為ウォームホィールとの歯形のかい離が大きくなり歯形方向 の歯当たりが非常に小さくなる。これは、発熱・騒音・振動の原因ともなる。		 又、問題はこれだけではない。ウォームホィールの加工コストには、ウォームホブのコストが責める比率が高い。このため、ホブに増径量を付ける ことは知られている。この増径量を多く付ければ、ホブが長持ちしてホィールのコストが安くなるが、径の大きなホブで歯切りされたホィールの 歯筋方向の歯当たりは増径量の大きさに反比例して小さくなる。１～２条ではそれほどではないが、３条になると非常に大きくなじみ運転をしなければ ならなくなる。

横転位設計について　(1)

横転位は、あまり一般的ではありませんが、現場での歯車加工の際、歯厚の調整方法として行われています。簡単に説明すると、ラック工具(ボブ)を工具軸方向に位相をずらして歯厚を減ずる方法です。本バージョンでは、歯厚を増加することもできる機能も備えています。たとえば、小歯車の歯厚を減らして、大歯車の歯厚を増加(マイナスを付ける)することが可能になりました。歯厚を増加する場合の加工では、ラック工具の歯厚を減らす必要があります。 強度計算の曲げ強度では、この結果を反映するように計算しています。
正面歯形における「法線方向歯厚増減量」か「ピッチ方向歯厚増減量」のどちらかのラジオボタンを選択して増減値を入力することによって横転位による歯形設計をすることができます。正の値を入力すると歯車の歯厚は減少します。マイナスを付けて入力すると歯厚は増加します。内歯車も同様です。
横転位設計　(2)  
a) 横転位量Hx
ラックと平歯車の噛み合い（正面歯形）に於いて、片方のラック歯形を軸方向に移動した（正面ピッチ方向歯厚増減量）時の歯厚減少量を歯直角に換算したものを横転位量Hxとする。
Hxa = Nx／COS α Hxa：正面ピッチ方向歯厚増減量
Hx = Hxa 　　　α：正面圧力角　

b) 法線方向歯厚増減量 Nx
Hxaを歯形法線方向に換算したものを法線方向歯厚増減量Nxとする。
Nx=Hxa・COS α　

c) 横転位係数 Xh
横転位量をモジュールmで除したものを横転位係数Xhとする。
Xh= Nx／(m・COS α)=Hxa／m

横転位量=Hxa